En particular, al analizar únicamente velocidades lineales no estamos considerando el spin generado dentro del análisis. De hecho, este modelo tiene mayor penetración en impactos del driver, en los que el spin generado es inferior. En particular, casi todos habremos oído mencionar en algún momento el concepto COR.
El COR (Coefficient of Restitution) ha sido utilizado y aún se menciona en muchos artículos como limitación impuesta a diseño de drivers. La realidad es que la USGA cambio esta limitación en 2004 para apoyarse en el “Characteristic Time Rating” (CTR) para definir los limites tecnológicos al diseño de palos. Aunque el CTR bien merece un artículo dedicado, en esta ocasión mencionar sus límites que son 239 microsegundos, más una tolerancia de 18 microsegundos en la medida.
En realidad, tanto el COR como el CTR pretenden poner un límite al efecto muelle que se genera durante el impacto. Si no hubiera ningún límite se tendería a impactos en los que no hubiera disipación de energía, dicho de otra forma, que toda la energía se convirtiera en energía cinética de las partes involucradas; por ejemplo, no habría disipación de energía por sonido en el impacto.
Ahora voy a introducir un análisis físico, repleto de ecuaciones, con objeto de profundizar en el modelo teórico. Os ruego encarecidamente que si el análisis físico-matemático os resulta complicado, no dejéis de leer la explicación final de lo que subyace en el sistema físico que se encuentra al final del artículo.
El análisis dinámico completo que se presentará a continuación se puede resumir con los siguientes pasos:
En primer lugar, planteamos ecuaciones de conservación de movimiento, en el que la velocidad que adquiere la bola es el resultado de la transmisión de cantidad de movimiento del palo a lo bola.
En segundo lugar, planteamos la ecuación de conservación de la energía, en la que se establece que, en ausencia de perdidas, la energía cinética de la cabeza del driver se convierte en energía cinética de la bola y energía cinética remanente en la cabeza del palo.
En tercer lugar, y quizás escondido en las ecuaciones lineales anteriores, se establece que no se ha generado energía cinética de rotación en la bola, es decir que no se ha generado spin. Aunque se puede considerar que esta parte no es válida, en realidad el modelo CTR actual considera impactos perpendiculares a la cara del palo, y por tanto es directamente aplicable.
En cuarto lugar, con estas asunciones deducimos que la máxima velocidad de la bola es la suma de la velocidad del driver antes y después del impacto. Esta parte será de especial interés en la explicación de los resultados que se encuentra al final del artículo.
En quinto lugar, sustituimos la ecuación de conservación de la energía por la relación entre velocidades establecidas por el concepto COR, y calculamos igualmente la velocidad de salida de la bola.
A continuación, pasamos a detallar las ecuaciones y os recordamos que consideramos de interés general los párrafos finales y vamos a ello sin más dilación.
Para el análisis vamos a considerar los siguientes elementos

Consideraremos dos ecuaciones diferentes, la conservación del momento cinético, y la conservación de la energía cinética.
La ecuación del momento cinético (Ecuación 1) nos dice:
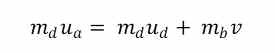
Que evolucionamos sucesivamente como sigue (Ecuación 1bis):
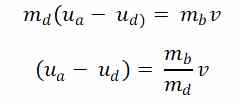
Esta ecuación la utilizaremos más adelante como ecuación 2
Por otra parte tenemos la ecuación de conservación de la energía cinética
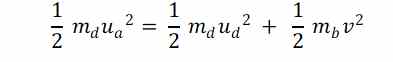
Que evolucionamos sucesivamente como sigue:
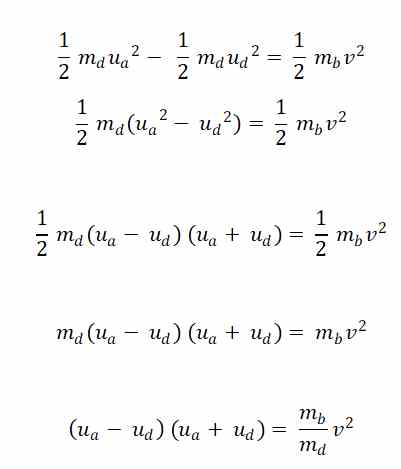
Y utilizando la ecuación 1 sustituimos el valor de la resta de velocidades
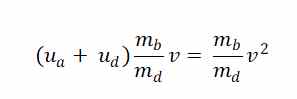
Luego:
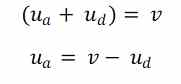
Aunque no he encontrado ningún sitio en el que explique el efecto muelle, me atrevo a decir que esta ecuación es la que mejor lo refleja. Esta ecuación nos dice que el máximo de diferencia entre la velocidad de la bola y la velocidad del driver tras el impacto es la velocidad inicial de driver. Además, si pasamos la velocidad del driver antes del impacto al lado derecho dividiendo tenemos lo siguiente:
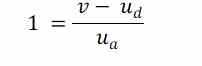
Esta ecuación es similar casi equivalente a la definición del COR
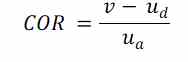
Como decía en este caso quedaría claro que el COR limitaría el efecto muelle.
Si reemplazamos la ecuación de conservación de energía, por el modelo del COR, podemos continuar resolviendo con la ecuación de conservación del momento cinético (Ecuación 1) y la ecuación del COR, de la que podemos extraer el valor de la velocidad del driver tras el impacto.
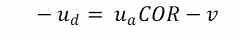
Y este valor lo sustituimos en Ecuación 1bis
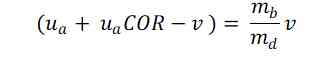
Y evolucionando
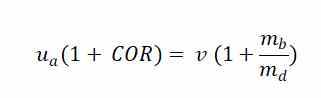
De donde podemos sacar el valor del smash factor (Velocidad de la bola dividido por Velocidad del driver antes del impacto), y lo referenciamos como Ecuación 3
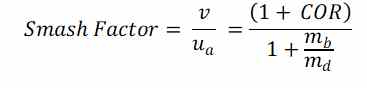
Para impactos de bola no perpendiculares a la cara del driver muchos (entre otros trackman) extrapolan la formula del smash factor a:
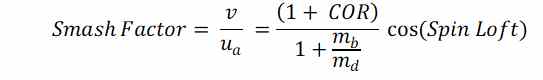
Si además comparamos el cuadrado de la velocidad de la bola según la Ecuación 3, para COR máximo igual a 1, y para COR máximo 0,83 que era la limitación de la USGA tendremos.
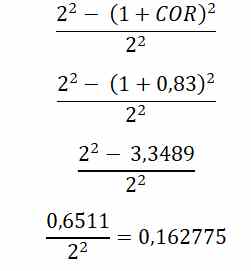
Luego, el porcentaje de energía cinética de la bola perdida por la limitación del COR seria 0,162775, o lo que es lo mismo, se conseguiría el 83,7225 % de la máxima energía cinética para COR = 1. Quizás por esto en algunos sitios se define el COR como el porcentaje de energía Cinética de la bola que se alcanza, pues como hemos visto esta igualdad se cumple para el COR 0,83 elegido en su momento por la USGA.
Como lo prometido es deuda, permitidme que intente explicar el fenómeno en palabras.
Inicialmente el driver viaja a una determinada velocidad, y estará en contacto con la bola del orden de 0,5 milisegundos. Como consecuencia del impacto, la velocidad final del driver habrá disminuido y será inferior. La fuerza del impacto estará rondando un cuarto de Tonelada para que os hagáis una idea de la intensidad de la percusión.
Vamos a partir el tiempo de impacto en dos mitades, e igualmente vamos a asumir que tras la mitad del intervalo, la velocidad del driver es justo la intermedia entre la velocidad final y la velocidad inicial de la cabeza.
Durante la primera mitad del intervalo, el driver está comprimiendo la bola, a la vez que la bola se está acelerando para pasar de velocidad cero, hasta un punto que alcanza la velocidad del driver (que a su vez va disminuyendo en el impacto).
En este punto medio de velocidad, en que la velocidad de la bola es igual a la velocidad del driver, la compresión adicional de la bola es imposible. La bola empieza a viajar a velocidad superior a la del driver, y la bola empieza a descomprimirse.
Cuando la bola se está descomprimiendo, la bola sigue en contacto en con el driver. En estos momentos no es le driver el elemento que presiona a la bola, sino al revés. Al descomprimirse como un muelle la bola esta empujando al driver, y a su vez por efecto de acción y reacción sigue propulsándose.
Si consideramos este segundo intervalo equivalente al primero, la bola seguirá acelerándose hasta aumentar su velocidad de nuevo en la media entre la velocidad inicial y la velocidad final del driver.
Si tomamos la definición del COR que hemos visto antes
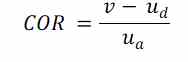
Y despejamos la velocidad final de la bola tendremos que la velocidad final de la bola es:
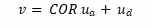
O lo que es lo mismo, que la velocidad de la bola, aparte el efecto del COR (COR = 1), es dos veces la media entre la velocidad inicial y velocidad final de driver:
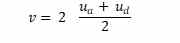
Espero que haya sido capaz de transmitiros al menos el modelo físico, y os ruego no dejéis de preguntar aquellas dudas que tengáis.
@agsmith
Comentarios en este hilo.
